| 1. | Ingkaran dari pernyataan, "Beberapa bilangan prima adalah bilangan genap." adalah ........ | ||||||||||
|
| 2. | Diketahui premis-premis: (1) Jika Badu rajin belajar dan patuh pada orang tua, maka Ayah membelikan bola basket. (2) Ayah tidak membelikan bola basket. Kesimpulan yang sah adalah ........ | ||||||||||
|
| 3. | Bentuk 3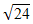 + 2 + 2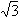 ( (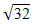 - 2 - 2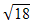 ) dapat disederhanakan menjadi ........ ) dapat disederhanakan menjadi ........ | ||||||||||||
|
| 4. | Diketahui ²log 7 = a dan ²log 3 = b, maka nilai dari 6log 14 adalah ........ | ||||||||||||
|
| 5. | Persamaan grafik fungsi kuadrat yang mempunyai titik balik minimum (1, 2) dan melalui titik (2, 3) adalah ........ | ||||||||||||
|
| 6. | Invers dari fungsi f(x) = 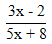 , x , x 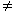 - -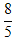 adalah f-1(x) adalah ........ adalah f-1(x) adalah ........ | ||||||||||||
|
| 7. | Bila x1 dan x2 penyelesaian dari persamaan 22x - 6.2x + 1 + 32 = 0 dengan x1 > x2 maka nilai dari 2x1 + x2 = ........ | ||||||||||||
|
| 8. | Himpunan penyelesaian dari pertidaksamaan eksponen: 92x - 4 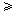 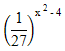 adalah ........ adalah ........ | ||||||||||||
|
| 9. | Akar-akar persamaan ²log² x - 6 . ²log x + 8 = ²log 1 adalah x1 dan x2. Nilai x1 + x2 = ........ | ||||||||||||
|
| 10. | Perbandingan umur Ali dan Badu 6 tahun yang lalu adalah 5 : 6. Hasil kali umur keduanya sekarang adalah 1.512. Umur Ali sekarang adalah ........ | ||||||||||||
|
| 11. | Persamaan garis singgung melalui titik A (-2, -1) pada lingkaran x² - y² + 12x - 6y + 13 = 0 adalah ........ | ||||||||||||
|
| 12. | Salah satu faktor suku banyak P(x) = x4 - 15x2 - 10x + n adalah (x + 2). Faktor lainnya adalah ........ | ||||||||||||
|
| 13. | Pada toko buku "Murah", Adi membeli 4 buku, 2 pulpen dan 3 pensil dengan harga Rp 26.000,00. Bima membeli 3 buku, 3 pulpen, dan 1 pensil dengan harga Rp 21.500,00. Citra membeli 3 buku dan 1 pensil dengan harga Rp12.500,00. Jika Dina membeli 2 pulpen dan 2 pensil, maka ia harus membayar ........ | ||||||||||||
|
| 14. | 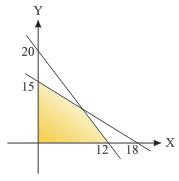 Daerah yang berwarna pada gambar merupakan himpunan penyelesaian suatu sistem pertidaksamaan linear. Nilai maksimum dari f(x, y) = 7x + 6y adalah ........ | ||||||||||||
|
| 15. | Seorang pembuat kue mempunyai 4 kg gula dan 9 kg tepung. Untuk membuat sebuah kue jenis A dibutuhkan 20 gram gula dan 60 gram tepung, sedangkan untuk membuat sebuah kue jenis B dibutuhkan 20 gram gula dan 40 gram tepung. Jika kue A dijual dengan harga Rp 4.000,00/buah dan kue B dijual dengan harga Rp 3.000,00/buah, maka pendapatan maksimum yang dapat diperoleh pembuat kue tersebut adalah ........ | ||||||||||||
|
| 16. | Diketahui persamaan matriks 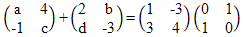 . .Nilai a + b + c + d = ........ | ||||||||||||
|
| 17. | Diketahui matriks P = 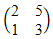 dan Q = dan Q = 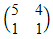 . Jika P-1 adalah invers matriks P dan Q-1 adalah invers matriks Q, maka determinan matriks P-1Q-1 adalah ........ . Jika P-1 adalah invers matriks P dan Q-1 adalah invers matriks Q, maka determinan matriks P-1Q-1 adalah ........ | ||||||||||||
|
| 18. | Diketahui vektor 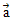 = 2t = 2t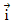 - - + 3 + 3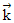 , , 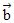 = -t = -t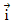 + 2 + 2 -5 -5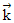 , dan , dan 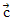 = 3t = 3t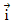 + t + t + + 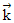 . Jika vektor ( . Jika vektor (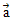 + +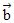 ) tegak lurus ) tegak lurus 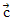 maka nilai 2t = ........ maka nilai 2t = ........ | ||||||||||||
|
| 19. | Diketahui vektor 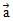 = = 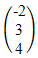 dan dan  = = 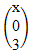 . Jika panjang proyeksi vektor . Jika panjang proyeksi vektor 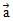 = = 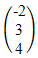 pada pada  adalah adalah 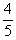 , maka salah satu nilai x adalah ........ , maka salah satu nilai x adalah ........ | ||||||||||||
|
| 20. | Persamaan bayangan parabola y = x² + 4 karena rotasi dengan pusat O (0, 0) sejauh 180° adalah ........ | ||||||||||||
|
| 21. | Persamaan bayangan garis 4y + 3x - 2 = 0 oleh transformasi yang bersesuaian dengan matriks 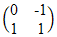 dilanjutkan matriks dilanjutkan matriks 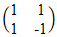 adalah ........ adalah ........ | ||||||||||||
|
| 22. | Diketahui suku ke-3 dan suku ke-6 suatu deret aritmatika berturut-turut adalah 8 dan 17. Jumlah delapan suku pertama deret tersebut sama dengan ........ | ||||||||||||
|
| 23. | Seutas tali dipotong menjadi 52 bagian yang masing-masing potongan membentuk deret aritmetika. Bila potongan tali terpendek adalah 3 cm dan yang terpanjang adalah 105 cm, maka panjang tali semula adalah ........ | ||||||||||||
|
| 24. | Diketahui deret geometri dengan suku pertama 6 dan suku keempat adalah 48. Jumlah enam suku pertama deret tersebut adalah ........ | ||||||||||||
|
| 25. | Diketahui kubus ABCD.EFGH dengan panjang rusuk 8 cm. Jarak titik H dan garis AC adalah ........ | ||||||||||||
|
| 26. | Diketahui kubus ABCD.EFGH dengan panjang rusuk 6 cm. Jika sudut antara diagonal AG dengan bidang alas ABCD adalah 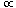 , maka sin , maka sin 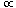 adalah ........ adalah ........ | ||||||||||||
|
| 27. | Diketahui segitiga MAB dengan AB = 300 cm, sudut MAB = 60° dan sudut ABM = 75°. Maka AM = ........ | ||||||||||||
|
| 28. | Jika tan 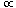 = 1 dan tan = 1 dan tan 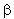 = = 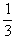 dengan dengan 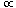 dan dan 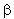 sudut lancip, maka sin ( sudut lancip, maka sin (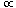 - - 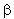 ) = ........ ) = ........ | ||||||||||||
|
| 29. | Nilai dari 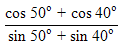 adalah ........ adalah ........ | ||||||||||||
|
| 30. | Himpunan penyelesaian persamaan cos 2x + 7 sin x - 4 = 0, 0° 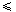 x x 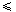 360° adalah ........ 360° adalah ........ | ||||||||||||
|
| 31. | Nilai dari 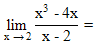 ........ ........ | ||||||||||||
|
| 32. | Turunan pertama dari 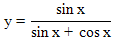 adalah y' = ........ adalah y' = ........ | ||||||||||||
|
| 33. | Diketahui f(x) = 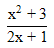 . Jika f '(x) menyatakan turunan pertama f(x), . Jika f '(x) menyatakan turunan pertama f(x),maka f(0) + 2f '(0) = ........ | ||||||||||||
|
| 34. | Sebuah kotak tanpa tutup yang alasnya berbentuk persegi, mempunyai volume 4 m³ terbuat dari selembar karton. Agar karton yang diperlukan sedikit mungkin, maka ukuran panjang, lebar, dan tinggi kotak berturut-turut adalah ........ | ||||||||||||
|
| 35. | Hasil dari 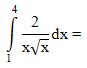 ........ ........ | ||||||||||||
|
| 36. | Hasil dari 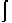 cos² x sin x dx adalah ........ cos² x sin x dx adalah ........ | ||||||||||||
|
| 37. | Luas daerah yang dibatasi oleh kurva y = -x² + 4x, sumbu x, garis x = 1, dan x = 3 adalah........ | ||||||||||||
|
| 38. | Volume benda putar yang terbentuk jika daerah yang dibatasi oleh kurva x - y² + 1 = 0, -1 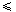 x x 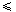 4, dan sumbu x diputar mengelilingi sumbu x sejauh 360° adalah ........ 4, dan sumbu x diputar mengelilingi sumbu x sejauh 360° adalah ........ | ||||||||||||
|
| 39. | Perhatikan data tabel berikut!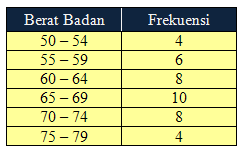 Kuartil atas dari data pada tabel adalah ........ | ||||||||||||
|
| 40. | Dua buah dadu dilempar undi secara bersamaan sebanyak satu kali. Peluang kejadian muncul jumlah mata dadu 9 atau 11 adalah ........ | |||||||||||
|
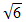
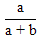
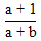
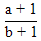
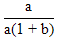
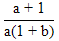
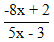
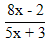
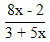
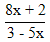
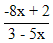
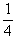
 }
}
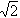 cm
cm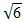 cm
cm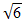 ) cm
) cm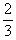
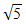
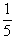
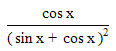

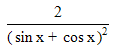
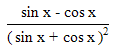

 satuan volume
satuan volume
Tidak ada komentar:
Posting Komentar